Game Theory, Economics of Productive Consumption, and Positional Investing
Game Theory, Economics of Productive Consumption, and Positional Investing
Abstract
This paper explores game-theoretical models derived from the Nash bargaining problem, reinterpreted through the lens of investment resource and opportunity dynamics. By applying principles from the economics of productive consumption, the study redefines Pareto optimality and introduces the concept of positional investing — the transformation of wealth into a privilege that suppresses others’ opportunities. The paper demonstrates how positional investing reduces system efficiency and distinguishes between cooperative and non-cooperative game structures. Practical implications include identifying conditions for successful reforms, especially in areas tied to human capability development, such as pension system sustainability. The findings suggest a paradigm shift from “economics of position” to an “economics of opportunity”.
1. Introduction

Figure 1 - An individual's freedom ends where another's money begins
Note: Vladimír Renčín (eminent Czech cartoonist)
2. Subject and Methodology
The paper presents the possibilities offered by a two-component model of supply and demand for investment resources and opportunities, incorporating theoretical foundations from productive consumption economics as an extension of neoclassical economics. It builds on earlier work , examining in greater detail the relationship between the neoclassical-based model and the productive consumption-based model. Unlike prior studies, it deduces positional investing through a deductive process from a refined definition of Pareto optimality in the market of investment resources and opportunities. The methods used include:
- A microeconomic model of supply and demand for investment resources and opportunities, expanded to include how investment opportunities are generated — a new element compared to previous theoretical outputs.
- Application of theoretical principles from productive consumption economics.
- Refinement of Pareto optimality definitions for both the original and expanded models.
- Identification and analysis of positional investing using original theoretical tools derived from the enhanced two-component model.
- Expression of the relationship between cooperative and non-cooperative strategies via two-matrix games, differentiated by Nash equilibrium types.
- For simplicity, the analysis focuses on two-player scenarios, without limiting the validity of the main conclusions.
Compared to previously published work, this paper advances research in productive consumption economics and positional investing by:
- Deriving positional investing from the supply and demand model, showing that it always involves suppressing or limiting the realization of investment opportunities for the disadvantaged player.
- Expanding the model to include the process of generating investment opportunities, allowing for identification and differentiation of various impacts of positional investing.
- Demonstrating that when this model is converted into normal-form games (specifically two-matrix games for two players), two distinct types of games emerge in terms of economic system efficiency: a) Games with positional investing resemble the Prisoner’s Dilemma, where system efficiency is significantly lower. b) Games without positional investing encourage cooperation, where Pareto and Nash equilibria coincide.
3. Main results
3.1. Comparison of Two-Component Graphs Based on Neoclassical Economics and the Economics of Productive Consumption
In the previous study two two-component models were presented:
- The first, by K. Binmore , illustrates the connection between the Edgeworth box diagram (describing marginal quantities in markets, commonly found in microeconomics textbooks) and a diagram in total quantities, which aligns with the Nash (S, d) bargaining problem. It is based on the theoretical assumptions of neoclassical economics.
- The second is a model developed by the authors, representing the financial market as the supply and demand of investment resources and investment opportunities. It draws on the theoretical foundations of the economics of productive consumption.
Understanding the relationship between these two models is crucial. At first glance, they may appear similar, yet they differ significantly. It may also seem that they address different domains:
- The first applies to any exchange, including contributions by subjects to joint ventures.
- The second applies specifically to creditor–debtor relationships, where one party supplies investment resources and seeks opportunities, while the other demands resources and offers opportunities.
In reality, the distinction is more nuanced. As Pigou noted, consumption can be viewed as an investment in personal productive capacity. That is, every act of consumption utilizes an investment opportunity. Compared to the neoclassical model, the productive consumption model is more general because:
- It considers the economic impact of consumption on the production process.
- It allows for increased system efficiency by enabling one subject’s resources to realize another’s more profitable opportunities, with the potential to share the resulting economic effect.
It’s no surprise that ideas focused on identifying the economic effects of consumption appear in the works of influential economists, both historical and contemporary. Neumann (1945–1946) transitioned to productive consumption economics by reducing all goods to “intermediate goods”; Friedman, in his Theory of the Consumption Function (1957) ; observed that households use current income to build assets — both human and non-human capital — to maximize the present value of future income (clearly inspired by Pigou). This direction is also reflected in modern works , , , , compare also .
Economics of Productive Consumption:
- Replaces the notion of a person as a “utility-maximizing consumer” with one who sees consumption as a productive process that develops capabilities as productive forces (e.g., for creative teams or contributing to society’s innovation potential). This represents a shift beyond mainstream economic theory.
- Shifts focus from how investment resources (financial capital) are created to how investment opportunities are generated — those that determine the dynamics and quality of economic growth and stem from human productive capabilities.
Viewed differently, the two-component model based on the Edgeworth box and Nash bargaining problem is a reduction of the investment supply–demand model, specifically by omitting:
- Income effects of consumption (i.e., consumption, like investment, affects future income).
- The possibility of credit relationships that enhance system efficiency by enabling one party’s resources to realize another’s more profitable opportunities.
When presenting both models, it’s important to highlight the fundamental differences in the variables they use. In the Nash bargaining model, the variables represent utilities aligned with consumer preferences. Nash (1951) , in his pioneering work on cooperative games, explicitly rejected the idea of comparing payoffs across players outside the game context. This is often interpreted to mean that interpersonal comparisons of payoffs do not influence strategy selection. One assumption of the Nash bargaining problem is that solutions are invariant under linear transformations—an axiom that does not hold in the financial market model presented here.
Another subtle but important difference: In consumer goods markets, each player is indifferent to the other’s utility. In financial markets, this assumption is too strong and limiting. Players consider each other’s income much more than in consumer exchanges.
From this perspective, neoclassical economics now serves as a “retiring foundation” for much of game theory, as reflected in ideas from Trockel’s co-authored article on Maskin’s monotonicity in social choice rules:
“There are several ways to factor the payoff vector function into an outcome function and a vector of utility functions. Two extreme cases are: (a) Treat the outcome space as identical to the strategy space, using the identity map as the outcome function and the payoff function as the utility function; (b) Treat the outcome space as the space of payoff vectors, using the utility function as a projection onto payoffs and the outcome function as the payoff vector function” .
Interpretation: In neoclassical economics, the central figure is the consumer who maximizes utility according to preferences. Preferences are typically expressed via indifference curves or, more generally, through the Neumann–Morgenstern axiomatization of preferences (from their 1944 Theory of Games and Economic Behavior). “Utility” is understood as a subjective experience. In most games, what is interpreted as payoffs (e.g., payoff matrices or vectors) is not “utility” in this sense, but another quantity — often money, but also time in prison (as in the Prisoner’s Dilemma), or outcomes in games or conflicts.
In the theoretical system based on productive consumption economics, payoffs always represent returns from combining investment resources and opportunities. This simplifies optimization tasks and opens new, important questions.
This insight is fundamental. It provides a more general theoretical basis for resolving issues of distributing returns from joint actions. It also raises the question: Why hasn’t this shift happened sooner? Why hasn’t a new space of problems emerged — requiring new concepts, tools, and methods with practical relevance? If our proposed approach is correct, we must answer that question too.
3.2. Pareto Optimality in the Model Based on Supply and Demand of Investment Resources and Opportunities, and Positional Investing
To grasp the essence of Pareto optimality in this context — where no one can improve their position without worsening another’s — we must consider a model based on the supply and demand of investment resources and opportunities. In such a model, opportunities are utilized according to their profitability and distributed so that everyone benefits, regardless of who owns the resources or the opportunities.
If opportunities are not used based on their profitability, it implies that less profitable ones are being realized while more profitable ones are ignored. Replacing the former with the latter increases total returns, which can then be shared — proving the original state was not Pareto optimal.
This optimal allocation reflects a natural tendency of societal development, prompting the question: what prevents its fulfillment? Logically, it must be something that obstructs the use of opportunities based on profitability. Moreover, this obstruction must benefit one player more than if they shared the returns fairly.
This is where the concept of positional investing comes in — defined as the transformation of wealth advantage into privilege, used by one party to discriminate against another , . This phenomenon permeates the economic system in various forms but shares a common foundation: suppressing the investment opportunities of the disadvantaged party to increase the profitability of the advantaged party’s own opportunities, even at the cost of overall system efficiency.
Understanding the role and mechanism of positional investing is essential to identifying the root causes of current economic problems. Defining and exposing this phenomenon is a major theoretical contribution. The way it reduces system efficiency will be demonstrated later.
Why Has Positional Investing Been Overlooked? The lack of attention to positional investing likely stems from two converging factors:
- Methodological: Advancing this area requires integrating multiple insights — interpreting productive consumption economics, applying cooperative game theory to investment markets, identifying positional investing, developing analytical tools, and uncovering the new research space of opportunity generation. These must be connected meaningfully to reveal conditions where Pareto and Nash equilibria coincide.
- Ideological: Positional investing — turning wealth into privilege and a tool of discrimination — is ideologically sensitive. Its general form involves suppressing the disadvantaged player’s opportunities, increasing the advantaged player’s returns while reducing system efficiency. Highlighting this issue and developing tools to analyze it may not be universally welcomed. A more “palatable” view might suggest that giving rule enforcers enough reward will prevent them from breaking the rules. The theory of positional investing refutes this notion.
3.3. Positional Investing and the Preconditions for Mutual Cooperation
When positional investing occurs, the overall volume of investment opportunities declines due to two distinct causes:
- More profitable investment opportunities of one player are replaced by less profitable ones belonging to the player who engages in positional investing.
- The total amount of investment resources in the system is reduced by the portion used by the positional investor to strengthen their position rather than to generate returns.
So far, we’ve considered only one aspect of the supply and demand model for investment resources and opportunities — namely, that new investment resources arise from combining existing resources with opportunities. But when considering mutual cooperation, it’s important to recognize that a similar principle applies to new investment opportunities, which emerge from the utilization of existing ones.
In a system where positional investing plays no significant role and opportunities are used based on their profitability, the generation of new opportunities becomes the most important source of income for players. This requires an expanded definition of Pareto optimality:
Investment opportunities are utilized and generated according to their profitability, regardless of who owns the existing or newly generated resources and opportunities.
On the basis of the above, we can compare the efficiency of an economic system based on the generation and exploitation of investment opportunities according to their rate of return, regardless of who owns the investment funds and who owns the investment opportunities (in Figure 2 on the left), with the efficiency of a system in which positional investing, i.e. the transformation of a property advantage into a privilege, into an instrument of discrimination against the other, operates (Figures 2–4).
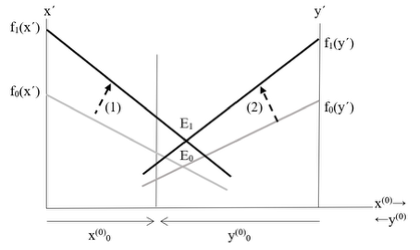
Figure 2 - How new investment opportunities are generated through the combination of existing resources and opportunities
x(0)→ left to right coordinates of the amount of investment resources of player X
←y(0) right to left coordinates of the amount of investment resources of player
x(0)0, y(0)0 default amount of investment resources of players X and Y
x´, y´ the coordinates of the marginal return from the combination of investment funds and investment opportunities
E0 the initial equilibrium point in the case of a functioning financial market
The grey colour indicates the initial situation given by the marginal return functions of the initial investment opportunities of players X and Y
f0(x´), f0(y´) marginal return functions from the combination of investment funds and investment opportunities of player X and player Y
(1), (2) arrows showing the shift of the marginal return functions from the newly generated investment opportunities of player X and player Y when the original investment opportunities are realized
The situation created by the combination of investment funds and investment opportunities:
f1(x´), f1(y´) the marginal revenue function from the combination of newly generated investment funds and newly generated investment opportunities of player X and Y
E1 the new equilibrium point in the case of a functioning financial market
The marginal revenue function from the combination of investment funds and investment opportunities of player X and Y is also a function of the supply or demand of investment funds and investment opportunities. In the given figure, player X, after depleting his own profitable investment funds, has more profitable investment opportunities than player Y, after depleting his investment funds, and therefore demands investment.
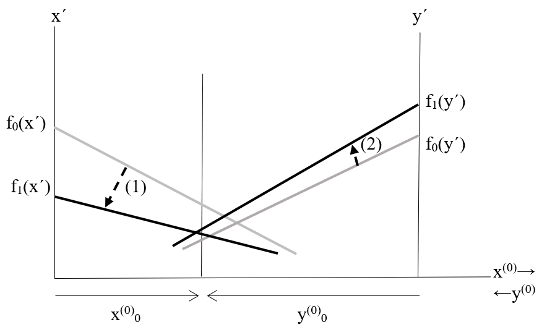
Figure 3 - Positional investing distorts this process, shifting marginal return functions and reducing overall efficiency
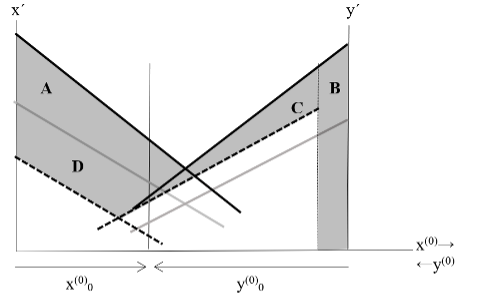
Figure 4 - Compares both systems and highlights four components of efficiency loss due to positional investing
A: Missed opportunities that could have been generated by player X.
B: Suppression of player X’s existing opportunities.
C: Lower returns for player Y’s opportunities compared to gains from suppressing X.
D: Sacrificed resources that could have supported cooperative opportunity generation.
In short, efficiency declines due to:
- Unproductive use of resources for positional investing (B).
- Limited or absent generation of opportunities for mutual benefit (A, C).
- Suppression of the disadvantaged player’s opportunities (D).
The need for a change in the view of the economic system from an ‘economics of positions’ to an ‘economics of opportunities’ will become commonplace quite quickly. There will be many advocates of the ‘old’ economics, those who will not be able to move beyond the inertial vision, but they will gradually diminish. At the same time, there will be a growing number of those who will see their opportunity in adopting and promoting the new view, both in theory and (very topical) in practice.
The difference between the systems on the left and right of Figure 3 is not only quantitative but also qualitative. We can translate the expressions of games with and without positional investing into the form of two-matrix games in normal form:
Table 1 - Initial scheme
Player Y | |||
1st strategy | 2nd strategy | ||
Player X | 1st strategy | x11 ; y11 | x12 ; y12 |
2nd strategy | x21 ; y21 | x22 ; y22 | |
Note: xij, yij are player payoffs
In general, there can be more players, more rounds more strategies.
In our case, we start from two extreme positions:
Full cooperation (K) strategy, i.e., none of the players uses positional investing.
A full non-cooperation strategy (N), i.e. the player who has the opportunity to do so uses positional investing.
Ad K: The strategy of full cooperation is easily and clearly defined in the language of supply and demand of investment funds and investment opportunities. It is a case where players exploit existing investment opportunities according to the overall rate of return on the investment opportunities generated, regardless of which player the investment opportunities are generated by and from which player's funds.
Ad N: The strategy of full non-cooperation is also easily and clearly defined in the language of supply and demand of investment funds and investment opportunities. A player uses investment funds to maximize his return through (taking advantage of) positional investing, given the other player's expected choice of strategy.
This allows a distinction to be made between prisoner's dilemma games, which correspond to games in which positional investment plays a significant role, and games in which the highest payoffs are obtained when players cooperate (KK). On this basis, KK situations can be identified that have occurred at different points in history, exist at present, or have been created for a certain period of time. Subsequently, the causes that have led or may lead to the change of a situation from KK to NN can be identified, which has important practical applications, which will be addressed in the discussion as this is a separate topic.
Historically, KK situations have emerged in various eras and contexts. Understanding what causes a shift from KK to NN has practical applications, especially in areas like pension system sustainability.
Application to Pension Reform; the findings highlight a key difference between:
- Restrictive approaches: Rely on administrative enforcement to maintain sustainability.
- Motivational approaches: Encourage all stakeholders to create conditions for extending productive engagement of pension system clients.
This is a standalone topic that demonstrates the power of connecting general theory with real-world practice.
4. Summary and Discussion
This paper explores game models analogous to the Nash bargaining problem, but instead of relying on Nash’s original framework, they are based on the supply and demand of investment resources and opportunities, drawing on the theoretical foundations of productive consumption economics. By defining Pareto optimality within this domain, the paper identifies the phenomenon of positional investing and develops tools to analyze its role — particularly its impact on the efficiency of economic systems.
From a practical standpoint, several key questions arise:
- Where do conditions emerge for games in which cooperation is beneficial — where Nash and Pareto equilibria coincide? This includes analyzing historical periods where such cooperative dynamics occurred. (This is currently a focus of our intensive research.) Understanding these conditions is crucial for initiating such games, which aligns with identifying prerequisites for successful reforms in areas where human capability development plays a central role.
- What risks threaten cooperative games, and what are the main causes of their breakdown (limitations, external pressures)? Answering this helps support cooperative dynamics, especially in reform efforts tied to human development.
- How can we model the relationship between cooperative games and their environment? Specifically, how can we increase the resilience of cooperative scenarios in environments dominated by positional investing? It turns out this relationship can be effectively modeled using two-matrix games in normal form.
To illustrate this research area, consider the challenge of stabilizing the pay-as-you-go pension system by creating incentives for individuals to extend their productive careers. Stakeholders who can be motivated to engage in cooperative games include not only clients (insured individuals), but also providers of productive services (education, healthcare, rehabilitation, corporate culture, etc.) and intermediaries (e.g. health insurers).
5. Conclusion
The issues addressed in this paper belong to a broader context of contemporary transformation — one that, despite historical twists and turns, is leading to the rise of productive services focused on utilizing and generating investment opportunities tied to the development, preservation, and application of human capabilities. In our view, this shift is comparable in scale and significance to the Industrial Revolution.
The more precisely we identify the key moments of this transformation, the better we can avoid the trap of outdated thinking — one that overlooks the role of positional investing and proposes restrictive solutions that not only fail to solve current problems but exacerbate them. Theoretically, this marks a transition from neoclassical economics to the economics of productive consumption.
